Προσομοίωση του πίνακα Smith μέσω ενός προγράμματος σε Java - Γενικές οδηγίες

 

ΠΡΟΣΑΡΜΟΓΗ

               Σε οποιοδήποτε σύστημα μετάδοσης, μια πηγή στέλνει ισχύ σε ένα φορτίο, όπως είναι για παράδειγμα μια κεραία. Ιδανικά, σχεδιάζουμε το δίκτυο μετάδοσης έτσι ώστε η χαρακτηριστική σύνθετη αγωγιμότητα της πηγής, της γραμμής μεταφοράς και του φορτίου να είναι ίσες. Δυστυχώς πολλές πραγματικές περιπτώσεις μας αποδεικνύουν πως κάτι τέτοιο είναι δύσκολο να επιτευχθεί στην πράξη. Για παράδειγμα , μπορεί να θέλουμε να χρησιμοποιήσουμε μια κεραία για ένα ευρύ φάσμα συχνοτήτων. Όμως η χαρακτηριστική σύνθετη αντίσταση της κεραίας είναι απίθανο να μείνει σταθερή με τη μεταβολή της συχνότητας, ειδικά αν το εύρος ζώνης είναι μεγάλο.

 Στην πραγματικότητα η επίτευξη μιας καλής προσαρμογής φορτίου είναι ένα από τα πιο συνηθισμένα προβλήματα της μικροκυματικής τεχνολογίας. Οι δύο παράμετροι εξάλλου που αποτελούν ένδειξη καλής προσαρμογής, δηλ. ο συντελεστής ανάκλασης ρ_L και ο λόγος στασίμων κυμάτων S( αλλά και το μέγεθος «εξασθένηση από επιστροφή»  L_R=20log|ρ_L|  ) εξαρτώνται από τη συχνότητα. Η προσαρμογή μπορεί να γίνει είτε μεταβάλλοντας τον τύπο της γραμμής μεταφοράς ( άρα και τα χαρακτηριστικά μεγέθη της διάδοσης ) είτε επιλέγοντας το κατάλληλο φορτίο =σύνθετη αντίσταση τερματισμού . Αν όμως τίποτα από αυτά δεν είναι πρακτικά εφικτό , τότε παρεμβάλλουμε μεταξύ πηγής και φορτίου κάποιες ειδικές προσαρμοστικές διατάξεις.

Σύντομη περιγραφή για τις γραμμές μεταφοράς και τους υπολογισμούς πάνω στο χάρτη Smith με βάση το πρόγραμμα εξομοίωσης

Όταν η σύνθετη αντίσταση της γραμμής μεταφοράς δεν ταιριάζει με αυτήν του φορτίου, τότε μέρος του μεταδιδόμενου προς το φορτίο κύματος ανακλάται πίσω στην πηγή. Το ανακλώμενο κύμα που έχει διαφορετικό πλάτος και φάση, υπερτίθεται στο προσπίπτον κύμα  και το άθροισμα ονομάζεται στάσιμο κύμα.

Το ανακλώμενο κύμα έχει σαν αποτέλεσμα το πλάτος του τελικού κύματος να μεταβάλλεται ως συνάρτηση της θέσης πάνω στη γραμμή μεταφοράς. Ο λόγος στάσιμου κύματος (SWR=Standing Wave Ratio), ο οποίος είναι ο λόγος μεταξύ του μέγιστου και του ελάχιστου πλάτους του συνολικού (στάσιμου) κύματος,χρησιμοποιείται για την εκτίμηση του πόσο καλή προσαρμογή επιτυγχάνεται . Ορίζεται συγκεκριμένα ως S=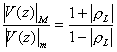, όπου ρ_L ο συντελεστής ανάκλασης στο τέλος της γραμμής μεταφοράς. Ο λόγος S λοιπόν ,με δεδομένο ότι 0≤ |ρ_L|≤1 ,θα είναι σε αυτή την περίπτωση μεγαλύτερος της μονάδας.

Αν δεν υπάρχει καθόλου ανακλώμενο κύμα, δηλ. η προσαρμογή φορτίου είναι τέλεια , το πλάτος του συνολικού κύματος θα είναι σταθερό για κάθε σημείο πάνω στη γραμμή μεταφοράς. Το αποτέλεσμα είναι να ισχύει SWR = 1 που σημαίνει μέγιστη μεταφορά ισχύος στο φορτίο. Ο SWR μπορεί να εκτιμηθεί μετρώντας το συντελεστή ανάκλασης στο δίκτυο. Ο αναλυτής δικτύου (network analyzer) είναι ένα εργαλείο που μας επιτρέπει να κάνουμε ακριβώς αυτό. Είναι ένα ειδικό πρόγραμμα που διανέμεται δωρεάν και μέσω Web από αρκετές εταιρείες.

Αν γνωρίζουμε το συντελεστή ανάκλασης μπορούμε επίσης να υπολογίσουμε την χαρακτηριστική σύνθετη αντίσταση φορτίου με χρήση του χάρτη Smith. Ο χάρτης Smith είναι ένας μοναδιαίος κύκλος εντός του οποίου είναι χαραγμένοι κύκλοι σταθερής αντίστασης r και τόξα σταθερής αντίδρασης x. Υποθέτουμε την εξίσωση για την ανηγμένη σύνθετη αντίσταση στη θέση ξ=l-z που είναι ζ(ξ)= r+jx =Z(ξ)/Z_o , όπου Ζ_ο η κυματική αντίσταση της γραμμής μεταφοράς που εξαρτάται από τα χαρακτηριστικά της εκάστοτε γραμμής. Η προκαθορισμένη τιμή της στο πρόγραμμα είναι Ζ_ο=50 Ohms . Να σημειωθεί ότι στο πρόγραμμα δεν εμφανίζονται οι ανηγμένες αλλά οι κανονικές τιμές των αντιστάσεων και αντιδράσεων της εκάστοτε σύνθετης αντίστασης φορτίου και οι τιμές τους αναγράφονται πάντα ως R και X. Οι αναλυτικοί τύποι που αναγράφονται για τα R και X είναι ουσιαστικά οι τύποι (3.47) του διδακτικού βιβλίου Μικροκυμάτων στη σελ.41

Αντίστοιχα για τον συντελεστή ανάκλασης η μιγαδική καρτεσιανή έκφραση είναι η ρ(ξ)=u+jv , όπου u και v οι μεταβλητές που αντιστοιχίζονται στον πραγματικό και φανταστικό άξονα του χάρτη Smith. Στο πρόγραμμα ειδικά ο συντελεστής ανάκλασης συμβολίζεται ως Γ ( gamma ) του οποίου οι τιμές μπορούν να επιλεγούν είτε διακριτά από τα μενού κάτω στην οθόνη είτε μετακινώντας τον κέρσορα με το ποντίκι σε οποιοδήποτε σημείο εντός του μοναδιαίου κύκλου.  Παρόλο που αρχικά ο χάρτης Smith εμφανίζεται πολύπλοκος , ωστόσο στην πορεία αναδεικνύεται η πρακτικότητα και χρηστικότητά του , και αυτό οφείλεται σε μεγάλο μέρος στο πρόγραμμα εξομοίωσης.

Ο χάρτης Smith μας επιτρέπει να «μεταφράσουμε» τον συντελεστή ανάκλασης σε σύνθετη αντίσταση. Πρώτα μετράμε τον συντελεστή ανάκλασης με έναν network analyzer ή χρησιμοποιούμε μια γνωστή δοσμένη τιμή. Ειδικά στο πρόγραμμα εξομοίωσης της Agilent εισάγουμε την τιμή του συντελεστή ανάκλασης σε καρτεσιανή μορφή. Πατάμε το κουμπί Play (τρίγωνο), και το πρόγραμμα θα απεικονίσει ένα κύκλο με ακτίνα ίση με το πλάτος του συντελεστή ανάκλασης και κέντρο το κέντρο του μοναδιαίου κύκλου (constant VSWR circle). Αν μετακινήσουμε τον συντελεστή ανάκλασης οπουδήποτε πάνω σε αυτό τον κύκλο, μπορούμε να δούμε από το κύμα στα αριστερά ότι το μέτρο του λόγου SWR μένει το ίδιο, μόνο η φάση του αλλάζει. Σε δεύτερη φάση και πατώντας το κουμπί Play ξανά το πρόγραμμα θα απεικονίσει τον κύκλο σταθερής αντίστασης  και το τόξο σταθερής αντίδρασης το σημείο τομής των οποίων δίνει τις συντεταγμένες του συντελεστή ανάκλασης που αντιστοιχεί στη συγκεκριμένη σύνθετη αντίσταση. (Οι πραγματικές τιμές υπολογίζονται και απεικονίζονται αριστερά στην οθόνη)

 (Οι μιγαδικές εκφράσεις για τον συντελεστή ανάκλασης , τόσο η καρτεσιανή όσο και η πολική απεικονίζονται διαρκώς πάνω αριστερά στην οθόνη και ανανεώνονται με κάθε αλλαγή που κάνουμε στην τιμή του Gamma )

Συνοψίζοντας τις μέχρι τώρα χρήσεις του χάρτη Smith πάνω στις γραμμές μεταφοράς , έχουμε να πούμε ότι ο χάρτης χρησιμοποιείται για τον γραφικό προσδιορισμό:

1.       Του συντελεστή ανάκλασης σε κάποιο σημείο μιας γραμμής μεταφοράς, αν είναι γνωστή η τιμή της αντίστοιχης σύνθετης αντίστασης.

 

2.       Την σύνθετη αντίσταση ή και τη σύνθετη αγωγιμότητα ( που αντιστοιχεί στο συμμετρικό - ως προς το κέντρο του μοναδιαίου κύκλου - σημείο ως προς το σημείο που παριστά τη σύνθετη αντίσταση ) με γνωστή την τιμή του συντελεστή ανάκλασης. Δηλ . πρώτα υπολογίζουμε την αντίστοιχη σύνθετη αντίσταση και μετά και και την σύνθετη αγωγιμότητα. Το τέχνασμα με το συμμετρικό σημείο είναι προφανές γιατί γίνεται. Γίνεται διότι ισχύει η σχέση ψ(ξ)=ζ(ξ)^-1=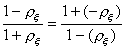 πράγμα που πρακτικά σημαίνει ότι το σημείο της σύνθετης αγωγιμότητας προκύπτει για την τιμή –ρ_ξ=e^j180ρ_ξ , δηλ. περιστροφή 180^ο  

 

3.       Τον λόγο στασίμων κυμάτων SWR που δεν είναι τίποτα άλλο από έναν κύκλο με ακτίνα ίση με το μέτρο του συντελεστή ανάκλασης . Όσο ο κύκλος αυτός προσεγγίζει μια τιμή ακτίνας ίσης με τη μονάδα , δηλαδή όσο ο συντελεστής ανάκλασης ρ_L τείνει στο μηδέντόσο πιο κοντά σε περίπτωση τέλειας προσαρμογής φορτίου βρισκόμαστε.

 

4.       Τον συντελεστή ανάκλασης σε οποιοδήποτε σημείο πάνω στη γραμμή μεταφοράς με γνωστή την τιμή του στο φορτίο, δηλ. το ρ_ξ  για κάποιο ξ με δοσμένο το ρ_L. Αυτό γίνεται με αναγωγή πάνω στο χάρτη Smith και με χρήση του δεδομένου ότι η τιμή του συντελεστή ανάκλασης φθίνει εκθετικά κατά μήκος μιας γραμμής μεταφοράς , δηλ. ρ_ξ=ρ_Le^-2γξ , όπου γ=α+jβ η σταθερά διάδοσης του κύματος. Η αναγωγή επομένως πάνω στο χάρτη Smith γίνεται με αξιοποίηση της σχέσης ρ_ξ=ρ_Le^-2αξe^-2jβξ. Βλ. και το διάγραμμα στη σελ. 42 των Μικροκυμάτων.

Παρατηρήσεις:

Πειραματιστείτε με τον εξομοιωτή παρατηρώντας τις τιμές της κυματομορφής της τάσης πάνω στη γραμμή μεταφοράς για z=0 έως και z=l (ανάλογα με τα διαγράμματα στη σελ. 39 του βιβλίου Μικροκυμάτων) και δείτε κατά πόσον μπορείτε να προβλέψετε τη μορφή του στάσιμου κύματος πριν μετακινήσετε τον  συντελεστή ανάκλασης. Κάθε φορά το πρόγραμμα μας δίνει τη δυνατότητα επαλήθευσης της διαίσθησής μας. Επίσης προσπαθήστε να απαντήσετε στα παρακάτω:

1.       Ποιο είναι το εύρος του SWR ;

2.       Ποια είναι η σπουδαιότητα του κέντρου του χάρτη Smith (του μοναδιαίου κύκλου) ;

3.       Ποιες υποθέσεις έχουν γίνει συνολικά για την γραμμή μεταφοράς ;

4.       Ποιες υποθέσεις έχουν γίνει συνολικά για την πηγή ;

Γενικές Οδηγίες για το «τρέξιμο» του συνοδευτικό προσομοιωτή της Agilent Technologies

Αυτός ο φασματικός αναλυτής είναι ένα διαδραστικό πρόγραμμα γραμμένο σε Java. Με τη βοήθειά του μπορούμε να κατανοήσουμε καλύτερα τη λειτουργικότητα του χάρτη Smith. Μπορείτε να τροποποιήσετε τις διάφορες παραμέτρους πατώντας τα κατακόρυφα κουμπιά. Τα 5 κουμπιά ελέγχου στην γωνία κάτω δεξιά χρησιμοποιούνται για να εκκινούν (τρίγωνο) και να σταματούν (τετράγωνο) την προσομοίωση, να προχωρούν στην επόμενη ή προηγούμενη ενότητα (διπλά τρίγωνα), και να μεταβάλλουν την ταχύτητα προσομοίωσης (+ και -). Αφού η προσομοίωση έχει τελειώσει , το κουμπί εκκίνησης μας μεταφέρει πάλι στην αρχή της όλης διαδικασίας.

Αν θέλετε να «τρέξετε» τον εξομοιωτή του χάρτη Smith κάντε κλικ στο παρακάτω κουμπί για να «κατεβάσετε» τα απαιτούμενα Java αρχεία στον δίσκο σας:     

·         Επίσης αν θέλετε περισσότερες οδηγίες σχετικά με το αντικείμενο και τη χρήση του χάρτη Smith , επισκεφθείτε το site της Agilent Technologies http://www.agilent.com/ όπως επίσης και τη σελίδα http://www.sss-mag.com/smith.html   ,όπου είναι δημοσιευμένα πολλά εργαλεία σχετικά με τον χάρτη Smith ενώ ειδικά για το σχεδιαστικό πακέτο ADS δείτε και τη σελίδα http://contact.tm.agilent.com/tmo/hpeesof/products/ads/adsoview.html